The basic methodology and the required equations for fillet weld size calculation is discussed in the previous article . It will be great if you go through the article before attempting to understand the welding joint design calculation example here.
Now let’s see how the weld design equations discussed in the previous article are applied here to find out the required welding size:
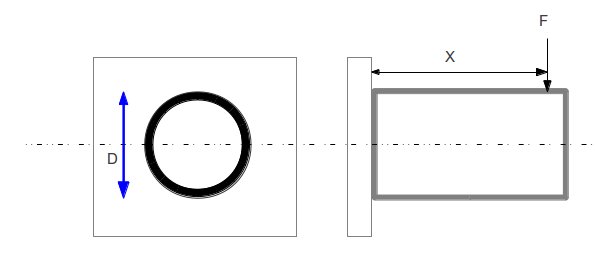
F= applied load = 20000 N
D = Diameter of tube = 200 mm
X = Distance = 100mm
- Unit throat length area (Au) of the welded joint is calculated from the eq.1 as below:
Au=3.14*D=3.14*200=628 sq.mm
- Design strength (Pw) is calculated from the eq.2 as:Pw=0.5*fu=0.5*430 = 215 N/sq. Mm
Where,
fu is the ultimate tensile stress of the parent material.
Assuming the parent material as S275 which has ultimate stress value (fu) 430 N/sq.mm.
- Unit area moment of inertia (Iu) for the circular welded area around the tube can be calculated asIu=3.14*(D/2)*(D/2)*(D/2)=3.14*200*200*200/8=3140000 mm3
Where,
3.14 is the value of PI.
- Direct shear stress (τs) for the fillet welded connection is calculated from the eq.3 as:τs=F/Au=20000/628=31.87 N/sq.mm
- Shear stress due to bending ( τb) is calculated from the eq.4 as:
τb=M*Y/Iu=F*X*0.5*D/Iu= 20000*100*0.5*200/3140000 = 63.69 N/sq.mm
Where,
M is the bending moment for the applied force
Y is the distance between the X-X axis and the extreme fibre of the welded cross section, it is radius for the circular cross section.
- Resultant stress (τ) can be found out after weld stress analysis calculation by using the eq.5 as:
τ=√(τs* τs + τb* τb)=(31.78*31.78+63.69*63.69)=71.17 N/sq.mm or MPa
- Weld throat size (t) to be calculated using the eq.6 like:
t= τ / Pw=71.17 / 215= 0.331 mm
- Weld leg length (L) need to be find out using the eq.7 as:
L=1.414*t = 1.414*0.331 = 0.468 mm
So, from the fillet weld size calculation example we found that the required minimum weld leg length to withstand the weld force is to be 0.468 mm, we will take the 3mm as the weld size for this example problem.
Hi, I am Shibashis, a blogger by passion and an engineer by profession. I have written most of the articles for mechGuru.com. For more than a decades i am closely associated with the engineering design/manufacturing simulation technologies. I am a self taught code hobbyist, presently in love with Python (Open CV / ML / Data Science /AWS -3000+ lines, 400+ hrs. )

you are a genius
The units do not work out…. t= tau/Pw = (N/ Sq mm) / (N/Sq mm) = unitless and not length. There are other issues as well, but I would revisit your analysis if I were you.
Nice try though.
The units do not work out…. t= tau/Pw = (N/ Sq mm) / (N/Sq mm) = unitless and not length. There are other issues as well, but I would revisit your analysis if I were you.
Nice try though.
Thanks for your comment.
Please see the previous article:
http://blog.mechguru.com/machine-design/fillet-weld-size-calculation-equations-for-welding-joint-subjected-to-bending-moment/
You will find that the “tau” and “Pw” is calulated based on unit throat sie in mm and hence by dividing “tau / Pw” you will get the throat size in mm.
It will be great if you tell what are the other issues, i can try to correct it.
No if you divide mm by mm you get dimensionless units. Bad math, sir.
“tau” is calculated as the total stress experienced by the welded joint for “UNIT” throat size. On the other hand “Pw” is the maximum permissible stress for the joint. So, to find out how many unit of throat size will require to resist the “Pw” you need to divide “tau/Pw”.
Or in other words, the unit of “tau” , actually, is (N/sq. mm)/mm or (N.mm/sq. mm).
Hope it make sense.
Awesome sauce! Now it makes perfect sense. Thanks for clarifying.
MechGuru, in actual, how can you find out the moment arm or the “x” in this computation?
If it is a point load applying then you can get “x” by directly finding the distance between the application point and welded joint face.
In case it is distributed load, then use center of gravity for calculating the “X”.
Have i answered you?
Should the first equation to be r 2 instead of D?
No, you have to take D as it will give you circumferential length of the weld sorrounding the circuler shaft
Hello, one thing i’m confused, after calculation, t=0.331mm, L=0.468mm, but why in your last sentence said the weld size is 3mm, not 0.331mm?
Weld size means weld throat size
your initial calculation of unit weld throat area is incorrect….. pi*D will give you the length of the weld and not area, though the theory about combined stress is correct, the calculation you have there is flawed.
Ref eq 5. Should the combined shear be 1/2 the bending stress squared added to direct shear squared then take the sq root of the sum? Total shear = sqrt [ (tb/2)^2 + (ts^2) ]
please letus also take instead of round shaft , if it is hollow shaft having inside hydro pressure, then euation ?
how to calculate it when there is torsion?
You may check this article
Step 3 should be mm^3 or am I missing something it is a unit calculation so it should be excluding the throat size?
You are right Brian, thank for pointing it out, corrected it.