Imagine you are driving, you suddenly see a obstacle in the middle of the road. Now, before you actually press the brake pedal, you, as a human being, will take some time for thinking or analyzing the situation. This time is called thinking time and the distance covered during this time is called thinking distance.
Actual breaking occurred after thinking time is over. The distance covered between the pressing of the brake pedal and stopping the car is called breaking distance.
So, technically,
Stopping distance = Thinking distance + Breaking distance ………………..eq.1
Now, the first term of the right hand side of the above stopping distance equation (eq.1) depends upon the state of mind of the driver and obviously varies from person to person.
However, as a rule of thumb,
Thinking distance = 3.33 x u …………………………….eq.2
Where,
u – Velocity at which the vehicle is moving at the instant when the brake is applied
Breaking Distance Calculation
As soon as you apply brake, the sliding friction between the tire and road comes into the picture.
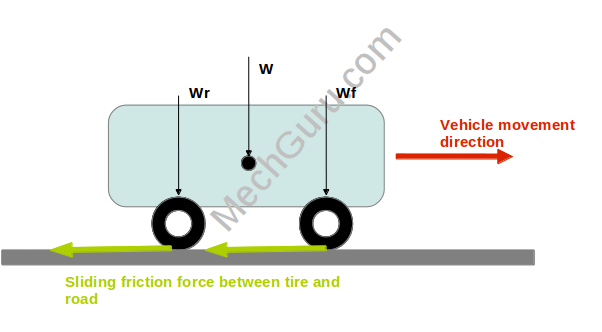
In this condition,
F = μs x Wf + μs x Wr = μs x (Wf + Wr )= μs x W = μs x m x g …………….eq.3
Where,
μs – Sliding coefficient of friction between tire and road
Wf – Vehicle weight on front wheel
Wr – Vehicle weight on rear wheel
W – Total vehicle weight
m – mass of the vehicle
g – gravitational acceleration
Also, from newton’s law,
F = m x a ……………………………………………….eq.4
Where,
a – Acceleration / deceleration of the vehicle
From the eq.3 and eq.4,
F = m x a = μs x m x g
⇒ a = μs x g …………………………………………..eq.5
Finally, we will require the following equation,
u2 = 2 x a x S …………………………………………….eq.6
Where,
S – Braking distance
u – Velocity at which the vehicle is moving at the instant when the brake is applied
a – Acceleration / deceleration of the vehicle
So, you can see from the eq.6, you can get the braking distance value. Combining this with the thinking distance value (eq.1 and eq.2) will get you the stopping distance. How? See the example below:
Example: Calculate the stopping distance of a car which is moving at a velocity of 60 KMPH. The car is moving on a dry asphalt road.
Solution:
Given data:
u = 60 KMPH = 16.67 Meter / hr
μs = Sliding coefficient of friction between rubber tire and dry asphalt road = 0.5
From eq.2,
Thinking distance = 3.33 x u = 3.33 x 16.67 = 55.5 Mtr.
From eq.5,
a = μs x g = 0.5 x 9.81 = 4.905 Mtr/sec2
From eq.6,
u2 = 2 x a x S
⇒16.672 = 2 x 4.905 x S
⇒ S = 28.32 Mtr.
From eq.1,
Stopping distance = Thinking distance + Breaking distance = 55.5 + 28.32 = 83.82 Mtr.
The above example shows how to calculate stopping distance of a car (or truck or any vehicle) using stopping distance formulas.
Hi, I am Shibashis, a blogger by passion and an engineer by profession. I have written most of the articles for mechGuru.com. For more than a decades i am closely associated with the engineering design/manufacturing simulation technologies. I am a self taught code hobbyist, presently in love with Python (Open CV / ML / Data Science /AWS -3000+ lines, 400+ hrs. )

Can you please help to put some article on Vehicle Brakes calculation when in Gradient ( Say 30 %) and how it is going to behave in terms of stopping distance , Force Required to stop the vehicle…