Blog

While designing the cantilever shaft (or any type of beam and shafts for that matter) we normally go ahead drawing the bending moment diagram to find the maximum bending moment value than creating the shear force diagram. Most of the time we ignore the maximum shear stress value for the shaft for the purpose of the shaft design calculation.  

Why we care (or scare) more for the maximum bending stress than the maximum shear stress value?

The reasons are

1. The value of the maximum shear stress is negligible compared to the maximum bending stress value in most of the cases of shaft (or beam) design.
2. And the maximum bending stress occurs at the extreme fiber from the neutral axis and the maximum shear stresses occur at the neutral axis.

 How?

Explanation:

Maximum bending stress equation for beams with rectangular cross section:

τb = (M*d)/(2*I)…………………..Eq.1

Maximum shear stress equation for beams with rectangular cross section:

τs=(3*F)/(2*b*d)…………………..Eq.2

Where,

M – Bending moment

F – Shear force

Y – Distance of the Area of interest from the neutral axis

I – Area moment of inertial of the area of interest

b – Width of the beam cross section

d – Depth of the beam cross section

Now let’s take an example of a rectangular cross section simple cantilever beam example to understand how the maximum bending and shear stress values are coming.

Example:

Let’s say the rectangular cantilever beam has the following input design data:

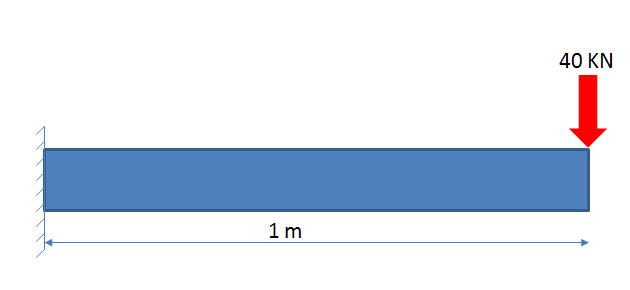
Applied load at the end =40 KN

Length of the beam = 1 m

Width of the beam cross section, b = 100 mm

Depth of the beam cross section, d = 300 mm

Explanation:

Maximum Shear force, F= 40 KN=40000 N

Maximum bending moment, M=40*1 =40 KN.M=40000000 N.mm

(You can take help of the SFD and BMD to calculate the maximum shear force and bending moment value)

Area moment of inertia, I=  100*300*300*300/12=225000000 mm⁴

Now, from the Eq.1 , the maximum bending stress value is

τb = 26.66666667 N/mm²

And, from the Eq.2, the maximum shear stress value is,

τs= 2 N/mm²

So, it is clear from the above example that how small is shear stress values as compared to the bending stress value in most of the cases.

Now let’s see the typical shear and bending stress distribution across the cross section for a rectangular section beam

Shear stress distribution:

For the beam with rectangular cross section,

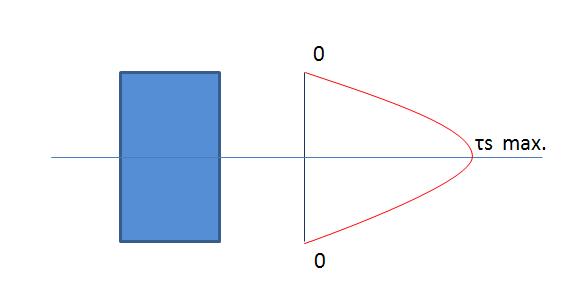
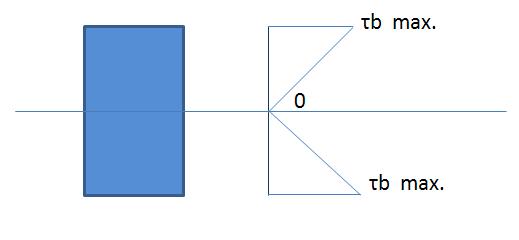
From the stress distribution plots above, you can observe that the maximum bending stress occurs at the extreme fiber and shear stress at the centre fiber.

So, if you sum up the shear and bending stress at different distances from the central axis then the maximum value of the sum will appear at the extreme fiber from the center and the value of the maximum sum of the two stress will be equal to the maximum bending stress value for the beam.  So, it is quite logical to ignore the maximum stress value in most of the cases of the shaft design.

References

Nptel

Shibashis Ghosh

Hi, I am Shibashis, a blogger by passion and an engineer by profession. I have written most of the articles for mechGuru.com. For more than a decades i am closely associated with the engineering design/manufacturing simulation technologies. I am a self taught code hobbyist, presently in love with Python (Open CV / ML / Data Science /AWS -3000+ lines, 400+ hrs. )