The complication of a stress system increases with increase of number of applied multi directional normal and shear stress. One very interesting and important fact about the complex stress system is that most of the time there will be one plane inclined with some angle with the vertical reference plane where normal stress will be maximum and shear stress will be zero and similarly there will be one more plane where normal stress will be zero and shear stress will be maximum, the first plane and stress perpendicular to the plane is called principal plane and principal stress respectively.
How you will be able to find the value of principal stress and orientation of principal plane?
We will discuss here.
For ease of discussion we will take example of a cube. Normal stresses (σx and σy) and shear stresses (Txy and Tyx) applied to the vertical and horizontal surfaces are shown in the figure below:
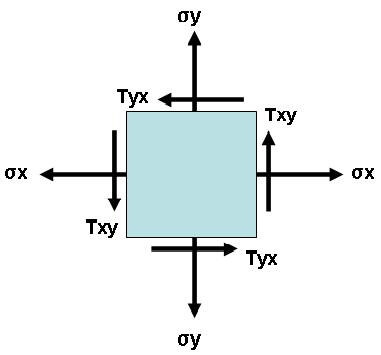
Please note that stresses σx and σy are the normal stresses applied on YZ and XZ surface of the cube respectively and they may or may not be the principal stresses.
Now there are infinite numbers of plane possible at different angles with respect to XZ surface of the cube and each of these planes will have different normal stresses and shear stresses as well. Let’s take a typical case of such plane (ab) which is inclined by an angle (θ) like below:
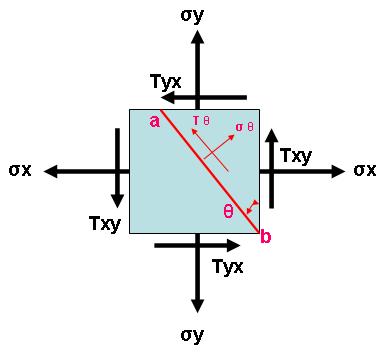
We assumed here that normal stress on the plane ab is σθ and shear stress is Tθ. Now remember the equilibrium equation we have studied during our graduations
∑Fx =0 and ∑Fy =0………..Eqn.1
By applying these well known equations here we can arrive two equations as below:
σθ = (σx + σy)/2+ [(σx – σy)/2](cos2θ )+ Txy(sin2θ)……..Eqn.2
Tθ = – [(σx – σy)/2] (sin2θ) + Txy(cos2θ)……..Eqn.3
You can use these Eqn.2 and Eqn.3 to find normal and shear stresses with respect to any plane at any angle with any to the surfaces of the cube and at the same time, there will be a certain value of θ where normal stress (σθ) will be maximum/minimum among all the possible normal stress values of all possible planes inclined at different angles. This maximum normal stress is called principal stress and the plane related to it is called principal plane. Similarly by using the same sets of equations you would be able to find a plane where shear stress (Tθ) will be maximum.
But how to find the equation of maximum and minimum?
Differentiate the Eqn.2 & Eqn.3 with respect to θ and equate it to zero. You will get the equations for maximum and minimum values.
The maximum and minimum normal stress (principal stress) will be:
σ max =( σ x + σ y )/2 + √{[( σ x – σ y )/2]2 + Txy2} ……..Eqn.4
σ max =( σ x + σ y )/2 – √{[( σ x – σ y )/2]2 + Txy2} ……..Eqn.5
tan2θ= Txy / [(σ x – σ y)/2]………….Eqn.6
Maximum shear stress will be:
Tmax = +/- √ {[(σ x – σ y)/2]2 + Txy2}………….Eqn.7
The planes where you will find maximum shear stress will be 450 away from the principal plane.
By further simplifying the Eqn.4, 5, 6 &7 we will get:
σ max = (σ x + σ y)/2 + Tmax ……..Eqn.8
σ min = (σ x + σ y)/2 – Tmax ……..Eqn.9
Tmax = (σ x – σ y)/2 ……..Eqn.10
So, as of now you are aware how to find principal stress, principal plane and maximum shear stress. But why should we find out the principal stress and maximum shear stress? Because by considering these stress values only we will go ahead with our further design calculations since these are the worst case values of stress.
Hi, I am Shibashis, a blogger by passion and an engineer by profession. I have written most of the articles for mechGuru.com. For more than a decades i am closely associated with the engineering design/manufacturing simulation technologies. I am a self taught code hobbyist, presently in love with Python (Open CV / ML / Data Science /AWS -3000+ lines, 400+ hrs. )

sir, i suppose that not stress but force is to be calculated on plane ab
Why do you think so?
Fantastic – Ramaswamy