Blog

We have already discussed how to design hydraulic cylinder piston.

In this sizing calculation tutorial we will see how to design hydraulic cylinder. Industrial hydraulic cylinder is an example of a typical thick cylinder.

 

Thick cylinder vs. thin cylinder

Cylinders in mechanical design are broadly classified into two categories:

1. Thin wall cylinder (R_i : t <10)
2. Thick wall cylinder(R_{i :} t >10)

Where,

R_i = inner radius of the cylinder

t = wall thickness of the cylinder

 

Hydraulic cylinder designing / sizing steps

 

Step 1: Find out internal radius of cylinder

Internal radius of cylinder, R_i = outer radius of the piston (which we already calculated here)

 

Step 2: Radial stress from Lame’s Theory

Lame’s Equation for calculating radial stress in a hydraulic cylinder at any given radius is:

Ϭ_r = ( b/ R²) – a …………….eq.2.1

 

Where,

Ϭ_r – Radial stress at radius R

a, b – Constants

 

 

 

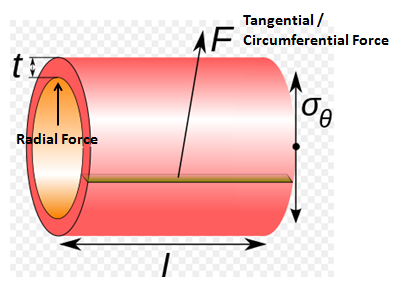
Step 3: Tangential stress

Lame’s equation for calculating tangential / circumferential stress at specified radius is:

Ϭ_c = (b/ R²) + a …………….eq.2.2

Where,

Ϭ_c – Tangential or circumferential stress at radius R

a, b – Constants

 

Step 4: Applying Boundary condition

Apply the given boundary conditions to the eq.2.1 & eq.2.2 to find out the constants a & b.

 

Some of the possible boundary conditions are:

• For R= Inner radius, Ϭ_r = Internal pressure of the cylinder
• For R= Inner radius, Ϭ_c =Max Permissible stress for the cylinder material

 

Step 5: Solve for the unknown

As the constants for both the equations are known now, you can easily find out the unknown quantity. We will see in the example, how?

 

Worked out example

Let’s take the same example as discussed in the piston design calculation tutorial with only additional input as external pressure= Atmospheric pressure

Find out the internal and external radius of the hydraulic cylinder.

Also find out the maximum stress in the cylinder.

 

Solution:

Input given:

Internal pressure, P₁ = 2 MPa (Gauge)

External pressure, P₂ = 0 MPa (Gauge)

Max. Permissible stress for cylinder material, Ϭ_max = 407.7 Mpa

Step 1:

We have already calculated, Inner radius, Ri = 12.5 mm (approx.)

 

Step 3:

We will apply following boundary conditions in the eq.2.1 & 2.2:

• For R= 12.5 mm, Ϭ_r =2 MPa
• For R= 12.5 mm, Ϭ_c =407.7 MPa

Solving we get,

• a = 153.85
• b = 39664.0625

By putting the values of the constants the equations become,

Ϭ_r = (39664.06/ R²) – 153.85 ……………………………..eq.2.3

Ϭ_c = (39664.06/ R²) + 153.85 ……………………………..eq.2.4

 

Step 4:

For finding out the thickness (or the outer radius) of the cylinder, we will use the following input conditions:

For R= required outer radius, Ϭ_r = Given external pressure = 0

 

Putting the above conditions in the eq.2.3 & 2.4 we get:

Required outer radius of the cylinder, R_o = 16.05 mm

 

In short, Lame’s equations of thick cylinder along with the given boundary conditions are used for calculating the design and sizing parameters of a hydraulic cylinder.