You are a structural design engineer and you are in task of designing a truss, the first thing you have to do is analysis of truss to find out the force applied at different joints and members of the truss.
Before going into details, I am assuming here that you are clear about the difference between frame and truss. In case you are not, please clarify it here.
Different types of trusses
All the trusses could be categorized in following three classes on the basis of stability:
• Statically stable truss: if a truss follow the following equation:
m >= 2j-r …………………………1.1
Where, m = total numbers of members in the truss
j = total numbers of joints
r = total numbers of reactions (normally 3 for statically determinate trusses)
And at the same time it has sufficient numbers of members to retain its shape when load is applied on any of the joints.
• Mechanism: when a truss is having the members less than the number specified by equation 1.1 (written above), then the truss is called mechanism.
• Statically indeterminate: Trusses which are having supports at more than two positions, it is called statically indeterminate truss. Member forces for these types of trusses could not be determined only by Newton’s laws.
Apart from the above classifications, trusses could be classified o the basis of shapes as well. Some of them are, common, scissors, flat etc.
Analysis of plane truss
We will limit our analysis of truss with statically determinate truss only. Also, the analysis will be based on following assumptions:
• The members carry only tensile or compressive force.
• The joints are of pin joint or hinged type, hence moment transfer by the members is negligible.
• Self weights of the members are negligible.
• Load acts only at the joints.
Analysis approach
• Write down the equilibrium equations (∑H=0, ∑V=0) for the truss as a whole and try to solve the reactions at supports.
• Now go on applying the equilibrium equations for each individual joints, start with the joint which is having two unknowns.
• At the end of successful analysis of the truss forces at all the members will be known.
• Use uniform sign conventions for tension and compression.
Example
Equivalent equations for the whole structure:
Va + Vb = 3x 10 Sin 60……………………………1.2
Ha = 3×10 Cos 60 = 15 …………………………………1.3
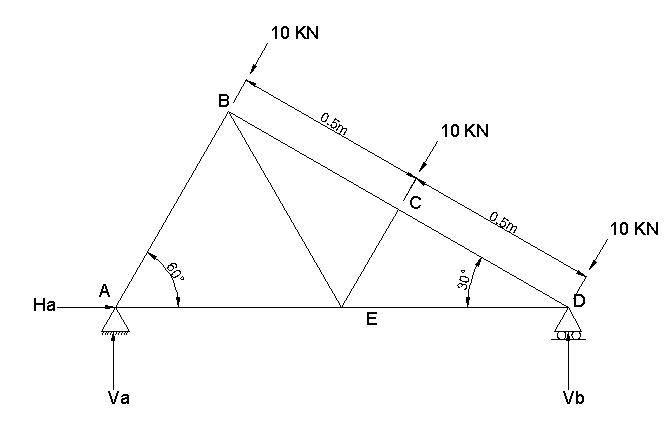
At, joint D:
The equilibrium equations will be:
Fde + Fcd Cos30 – 10 Cos60=0…………………………………..1.4
Vb-10 Sin 60- Fcd sin 30=0……………………………………….1.5
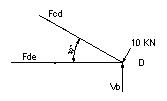
At joint A:
15 – Fab Cos60+Fae=0
Or, 0.5 Fab – Fae= 15 ………………………………1.6
Va – Fab Sin60=0
Or, Va- 0.866 Fab=0 ……………………………….. 1.7
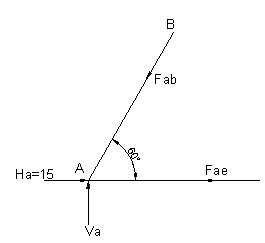
At joint B:
Fab Cos30+ Fbe Cos30+ Fbd Cos60 – 10 Cos30=0
Or, Fab + Fbe + 0.577 Fbd=10 ………………………….1.8
Fab Sin30 – Fbe Sin30- Fbd Sin 60-10 Sin 30=0
Or, Fab- Fbe- 1.732 Fbd= 10 …………………………….1.9
From Eq 1.7 & 1.8, we can get:
2 Fab -1.155 Fbd = 20
Or, Fab- 0.5775 Fbd =10 ………………………………..1.10
Fbe + 1.154 Fbd=0……………………………………….1.11
At joint C:
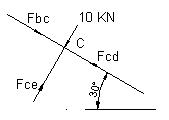
Fbc Cos30 + Fce Cos60- Fcd Cos30- 10 Cos60=0
Or, Fbc + 0.634 Fce – Fcd = 6.34 ………………………..1.12
Fbc Sin 30 + 10 Sin60 – Fcd Sin30 – Fce Sin30=0
Or, Fbc – Fce – Fcd = – 1.732 ……………………………1.13
At joint E:
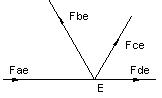
Fae + Fde + Fce Cos60- Fbe Cos60=0…………………….1.14
Fbe Sin60 +Fce Sin60=0 ………………………………….1.15
In order to find all the parameters of this problem, we will try to write the values of all the parameters by means of Vb.
From eqn. 1.5 we can write:
Fcd= 2Vb -1.732……………………2.1
From eqn. 1.7 we can write:
Fab= 1.154 Va= 1.154 (25.98-Vb)…….2.2
From eqn. 1.4 & 2.1 we can write:
Fde= 1.999-1.732Vb………………..2.3
From eqn.1.12 & 1.13 we can write:
Fce= 4.94………………………….2.4
From eqn.1.3 we can write:
Fbc= 1.476+ 2 Vb…………………2.5
From eqn.1.15 we can write:
Fbe=-4.94…………………………2.6
From eqn. 1.14, 2.4, 2.6 & 2.3 we can write:
Fae= -2.941 + 1.732 Vb……………2.7
From eqn.1.11 & 2.6 we can write:
Fbd=4.279………………………….2.8
From eqn. 1.10 & 2.8 we can write:
Fab=2.387………………………….2.9
Now, from eqn. 2.2 & 2.9 we can write:
Vb=225.766………………………..2.10
From, eqn. 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9& 2.10 we will find the force values in all the members:
Fcd= 2×225.766-1.732= 449.8 KN
Fab= 2.387 KN
Fde= -389.027 KN
Fce= 4.94 KN
Fbc= 453.008 KN
Fbe= -4.94 KN
Fae= 388.085 KN
Fbd= 4.279 KN
Analysis of truss for finding the force values in all the members is the first and most important part for structural design. By using Newton’s laws we can determine the force values off all the members. We have discussed a typical example of analysis of truss, the same methodologies can be used for all statically determinate trusses.
Hi, I am Shibashis, a blogger by passion and an engineer by profession. I have written most of the articles for mechGuru.com. For more than a decades i am closely associated with the engineering design/manufacturing simulation technologies. I am a self taught code hobbyist, presently in love with Python (Open CV / ML / Data Science /AWS -3000+ lines, 400+ hrs. )
