In first part of the flywheel design calculation tutorial example, we saw about calculating required mass moment of inertia for a particular application.

Flywheel design doesn’t stop with that. Its size, shape and material density / mass and maximum stresses are also to be taken into account while designing a flywheel. Which we will discuss in this part.

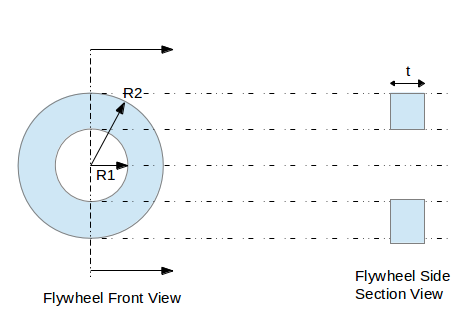
R1 = Flywheel inner radius

R2 = Flywheel outer radius

Step-1: Material selection

The material of flywheel on most applications will be either cast iron or cast steel.

The Density of the materials (d) is as follows.

Cast iron – 7250 kg/m³

Cast steel – 7800 kg/m³

Step-2: Calculation of the flywheel mass

We already know how to get the mass moment of inertia of a flywheel (I) required for a specific application.

Another equation for calculating the mass moment of inertial (I) is:

I = m* K²

Or, I = m* (R1² + R2²)/2………………..eq.2.1

R2 = 400 mm (assumption)

R2= 1.5 * R1 (assumption)………………eq.2.2

Where,

I = Mass Moment of Inertia of flywheel

m = Mass of the flywheel

K = Radius of gyration

R1 = Inner radius of flywheel

R2 = Outer radius of flywheel

From eq.2.1 mass of the flywheel can be calculated, how? Will discuss with the example later.

Step-3: Size and shape calculation

m = π * (R2² – R1² ) * t * d ……………………..eq.2.3

Where,

m = mass (will be obtained from step-2)

d = Density (will be obtained from Step-1)

t = Thickness of the flywheel

From the eq.2.2, 2.3 the cross section, size and thickness of the flywheel can be calculated.

Step-4: Stresses in the flywheel

Maximum stress (tangential) of a flywheel is given by:

Ϭ_t-max = (d/4)*(ω²)*[(3+v)*R2² + (1-v)* R1²]…………..eq.2.4

FOS = ω_yield / ω ………….eq.2.5

Where,

Ϭ_t-max = Max internal stress in the flywheel [ N/m² ]

d = Density of flywheel material [kg /m³]

ω = Angular velocity of the flywheel [rad/sec]

v = Poisson ratio of the flywheel material

FOS = Design factor of safety

ω_yield = Possible angular velocity when maximum internal stress equals to yield stress of the material

Example

Let’s take the same example discussed in Part-1 and find out the mass, size, shape and design parameters as per the equations discussed above.

Solution:

Step-1: density

We will select cast steel for our application, so

Density, d = 7800 kg/m³

Step-2: Mass

From Part-1,

I = 3.43 kg.m²

Using eq.2.1, eq.2.2 and using R1=0.4 m

Mass of flywheel, m= 29.68 kg

Step-3: Size & shape

Outer radius of the flywheel, R2 = 400 mm (given)

From eq.2.2,

Inner radius of flywheel, R1= 266.67 mm

From eq.2.3,

Thickness of flywheel, t=13.62 mm

Step-4: Stresses & FOS

From eq.2.4

Along with flywheel angular velocity from Part-1, as ω=1000 rpm = 2*π*1000/60= 104.67 rad/sec

And assuming Poisson’s ratio, v=0.4

Max. stress in the flywheel, Ϭ_t-max = 12533445.38 N/m² = 12.53 MPa

Assuming, Ϭ_yield = 150 MPa

Max speed at yield stress, ω_yield = 362.10 rad/sec

From eq.2.5,

FOS = 362.10 / 104.67 = 3.45

The ω_yield gives the critical speed of the flywheel.

This flywheel design and sizing calculation shows how to find out mass, size, cross section, maximum internal tangential stress and factor of safety for a flywheel.